What is it?
A Merkle tree is a tree in which each "leaf" is a hash of a block of data, and other nodes are hashes of concatenated hashes of their children. A hash tree allows efficient verification of large amounts of data (e.g. BitTorrent and the Bitcoin blockchain use this data structure). Merkle trees are commonly used in P2P networks because you only need a Merkle root (root hash) from a trusted source to verify data, and if one of the chunks is invalid, you don't need to download the entire data, just that chunk.
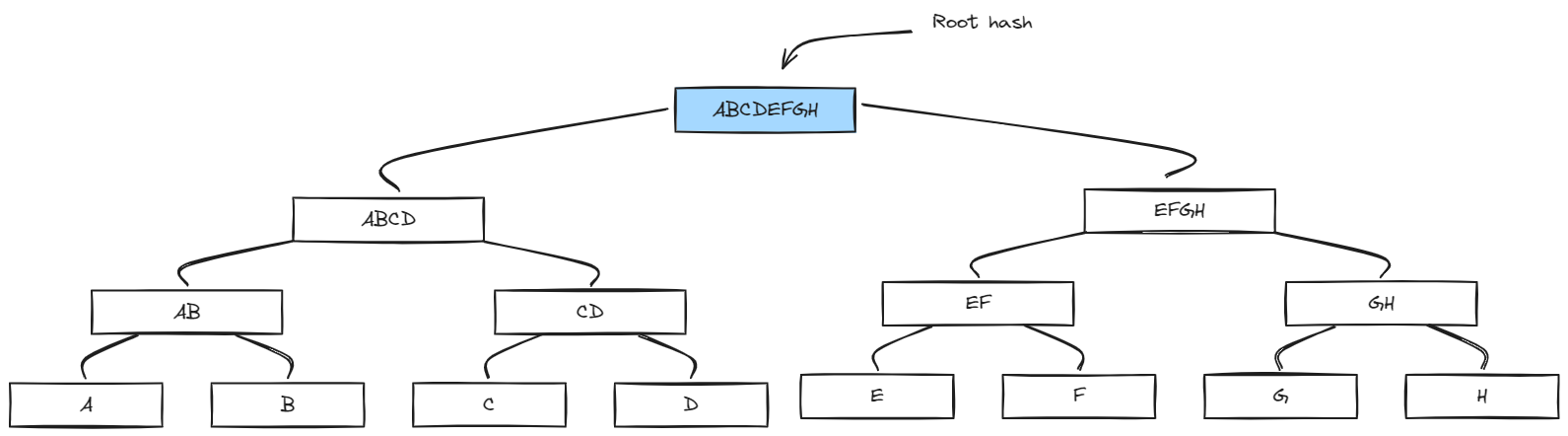
Merkle Proof
Merkle Proof is an algorithm used to verify chunks of data (leafs of the Merkle tree). Because of this algorithm, you only need to re-download data chunks that are invalid instead of re-downloading the entire file. To verify a leaf, you need hashes of the siblings of nodes on the root from leaf to root node (Merkle path).
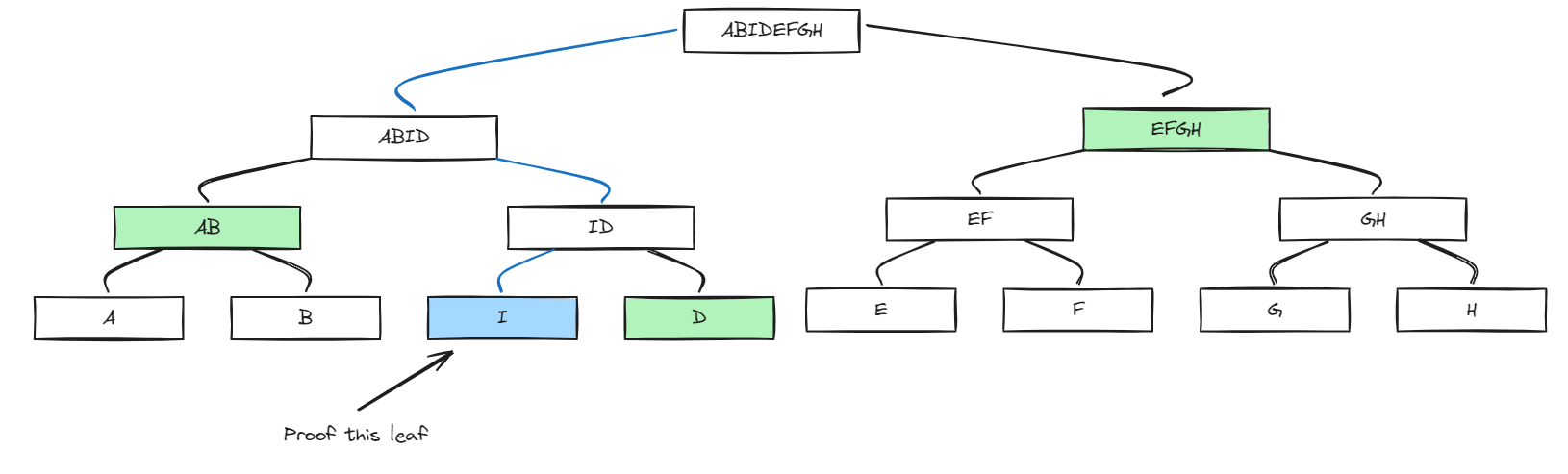
For example, we have a Merkle tree like the one above. We want to verify leaf `I`. We will only need `[D, AB, EFGH]` hashes because we can then get the root hash.
ID=hash(I+D)
ABID = hash(AB + ID)
Root hash = hash(ABID + EFGH)
When we calculate the root hash with our hash of the leaf, we can now compare this hash with the root hash from the trusted source, and if these hashes match, then our leaf is valid.
Example implementation in JavaScript:
import { hash } from 'node:crypto';
class MerkleTree {
constructor(leaves) {
if(leaves.length === 0)
leaves.push('');
const n = Math.pow(2, Math.ceil(Math.log2(leaves.length)));
for(let i = leaves.length; i < n; i++) {
leaves.push('');
}
this.leaves = leaves;
this.layers = [
this.leaves.map((leaf) => (hash('sha256', leaf)))
];
this.createTree();
}
createTree() {
let i = 0;
while(this.layers[i].length > 1) {
this.layers.push([]);
for(let j = 0; j < this.layers[i].length; j += 2 ) {
this.layers[i+1].push(hash('sha256', this.layers[i][j] + this.layers[i][j+1]));
}
i++;
}
}
getRootHash() {
return this.layers[this.layers.length - 1][0];
}
getProof(leafIndex) {
let index = leafIndex;
if(leafIndex >= this.layers.length)
return [];
let proof = [];
for(let i = 0; i < this.layers.length - 1; i++) {
const layer = this.layers[i];
const isRightNode = index % 2;
const pairIndex = isRightNode ? index - 1 : index + 1;
proof.push({
val:layer[pairIndex],
isRightNode: !isRightNode
});
index = index / 2 | 0; // Binary operator used for parsing to int
}
return proof;
}
verify(proof, leafIndex, root) {
const leaf = this.layers[0][leafIndex];
let hashVal = leaf;
for(let i = 0; i < proof.length; i++) {
hashVal = proof[i].isRightNode ? hashVal + proof[i].val : proof[i].val + hashVal;
hashVal = hash('sha256', hashVal);
}
return hashVal === root;
}
}
const leaves = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'];
const myLeaves = ['A', 'B', 'I', 'D', 'E', 'F', 'G', 'H'];
const tree = new MerkleTree(leaves);
const trustedRootHash = tree.getRootHash();
const myTree = new MerkleTree(myLeaves);
const proof = tree.getProof(2);
console.log(myTree.verify(proof, 2, trustedRootHash));